Charging Capacitor Voltage Equation
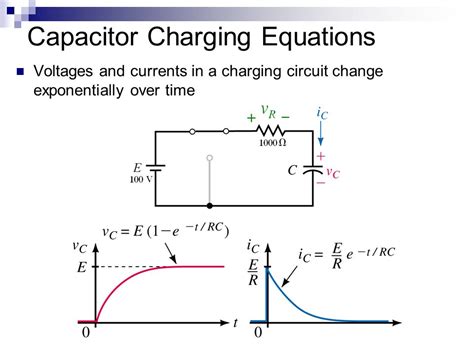
The process of charging a capacitor is a fundamental concept in electronics, and understanding the voltage equation is crucial for designing and analyzing circuits. When a capacitor is connected to a voltage source, it begins to charge, and the voltage across its plates increases over time. The rate at which the capacitor charges depends on several factors, including the capacitance value, the voltage of the source, and the resistance in the circuit.
One of the key equations in understanding the charging process of a capacitor is the voltage equation, which relates the voltage across the capacitor to time. This equation is derived from the fundamental principles of circuit analysis and is essential for calculating the voltage at any given time during the charging process.
The voltage equation for a charging capacitor is given by:
Vc(t) = Vcc * (1 - e^(-t/RC))
where: - Vc(t) is the voltage across the capacitor at time t, - Vcc is the supply voltage (the voltage of the source), - e is the base of the natural logarithm (approximately 2.718), - t is the time in seconds, - R is the resistance in the circuit, and - C is the capacitance of the capacitor.
This equation shows that the voltage across the capacitor increases exponentially with time, asymptotically approaching the supply voltage Vcc. The time constant (τ) of the circuit, which is the product of the resistance R and the capacitance C (τ = RC), determines how quickly the capacitor charges. The smaller the time constant, the faster the capacitor charges.
To illustrate the concept more clearly, let’s consider an example. Suppose we have a capacitor with a capacitance of 100 μF connected in series with a resistor of 1 kΩ to a 10V power source. We want to find the voltage across the capacitor 2 seconds after the switch is closed.
First, calculate the time constant of the circuit: τ = RC = 1000 Ω * 100 μF = 0.1 seconds
Then, use the voltage equation to find the voltage across the capacitor at t = 2 seconds: Vc(2) = 10V * (1 - e^(-2⁄0.1))
Calculating the value: Vc(2) = 10V * (1 - e^(-20)) Vc(2) ≈ 10V * (1 - 2.06 * 10^(-9)) Vc(2) ≈ 10V * 0.99999999794 Vc(2) ≈ 9.9999999794V
This means that after 2 seconds, the voltage across the capacitor is very close to the supply voltage, indicating that the capacitor is almost fully charged.
The charging capacitor voltage equation is a powerful tool for analyzing RC circuits and understanding how capacitors behave in different configurations. By applying this equation, engineers and technicians can predict the behavior of capacitors in a wide range of applications, from simple filters to complex power supplies.
How Capacitors Charge
The process of a capacitor charging involves the movement of electrons. When a capacitor is connected to a voltage source, electrons are pushed onto one plate of the capacitor and removed from the other, creating an electric field between the plates. As more electrons accumulate on one plate and are removed from the other, the voltage across the capacitor increases. The rate at which electrons move onto and off the plates depends on the resistance in the circuit and the capacitance of the capacitor.
The charging process can be divided into several stages, each characterized by different rates of voltage increase across the capacitor. Initially, when the switch is first closed, the voltage across the capacitor rises rapidly as electrons begin to move onto and off the plates. As the capacitor continues to charge, the rate of voltage increase slows down because the electric field established across the capacitor opposes further electron movement.
Time Constant and Charging Time
The time constant (τ = RC) is a critical parameter in determining how long it takes for a capacitor to charge. The time constant represents the time it takes for the voltage across the capacitor to reach about 63.2% of the supply voltage. After 2 time constants, the capacitor will be charged to about 86.5% of the supply voltage, after 3 time constants to about 95%, and after 5 time constants, the capacitor is considered fully charged, having reached about 99.3% of the supply voltage.
Understanding the time constant and its relationship to the charging time is essential for designing circuits where the charging and discharging of capacitors play a critical role. For instance, in power supply circuits, capacitors are used to filter out ripple voltage, and their charging time affects the overall performance of the supply.
Practical Applications
Capacitors and their charging characteristics are fundamental components in a wide range of electronic devices and systems. From the power supplies of computers and smartphones to the audio filters in sound equipment, capacitors play a crucial role in controlling voltage and current. In medical devices, such as defibrillators, capacitors are used to store energy that can be released quickly when needed. In automotive systems, capacitors are used for filtering and smoothing voltage fluctuations.
The ability to accurately model and predict the charging behavior of capacitors is essential for the design and optimization of these systems. By applying the charging capacitor voltage equation and understanding the principles of RC circuits, engineers can develop more efficient, reliable, and cost-effective electronic solutions.
Conclusion
The charging capacitor voltage equation is a foundational principle in electronics that describes how a capacitor charges over time when connected to a voltage source. This equation, Vc(t) = Vcc * (1 - e^(-t/RC)), provides a crucial tool for analyzing and designing circuits that involve capacitors. By understanding the time constant of the circuit and how it affects the charging time, engineers can better design and optimize electronic systems that rely on the charging and discharging of capacitors. As electronics continue to evolve and play an increasingly vital role in modern technology, the importance of mastering the principles of capacitor charging will only continue to grow.
What is the formula for the voltage across a capacitor during charging?
+The voltage across a capacitor during charging is given by the formula Vc(t) = Vcc * (1 - e^(-t/RC)), where Vc(t) is the voltage across the capacitor at time t, Vcc is the supply voltage, e is the base of the natural logarithm, t is the time in seconds, R is the resistance in the circuit, and C is the capacitance of the capacitor.
What does the time constant in an RC circuit represent?
+The time constant (τ = RC) in an RC circuit represents the time it takes for the voltage across the capacitor to reach about 63.2% of the supply voltage. It is a measure of how quickly the capacitor charges or discharges.
How long does it take for a capacitor to fully charge?
+A capacitor is considered fully charged after 5 time constants (5τ), at which point it has reached about 99.3% of the supply voltage. However, for most practical purposes, a capacitor is considered charged after 3 to 4 time constants.
In conclusion, the charging capacitor voltage equation and the concepts surrounding RC circuits are fundamental to the design and analysis of electronic circuits. Mastering these principles allows for the development of efficient, reliable, and innovative electronic systems that underpin modern technology. Whether in power supplies, filters, or timing circuits, the behavior of capacitors during charging is a critical aspect of circuit design, and understanding this behavior is essential for advancements in electronics and beyond.



